Tag: Python

Today, we’re going to wrap up our discussion of iterated function systems by looking at an algorithm which may be used to generate fractal images.

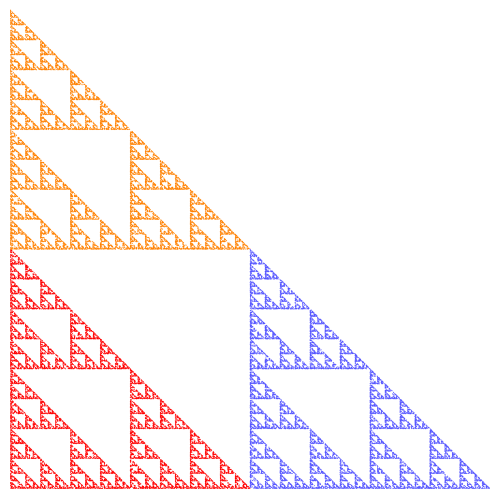
Recall (look back at the first post if you need to!) the Sierpinski triangle.  No matter what initial shape we started with, the iterations of the function system eventually looked like the Sierpinski triangle.

But there’s a computational issue at play.  Since there are three different transformations, each iteration produces three times the number of objects.  So if we carried out 10 iterations, we’d have 3¹⁰ = 59,049 objects to keep track of. Not too difficult for a computer.

But let’s look at the Sierpinski carpet. With eight different transformations, we’d have 8¹⁰ = 1,073,741,824 objects to keep track of. Keeping track of a billion objects just isn’t practical.

Of course you could use fewer iterations — but it turns out there’s a nice way out of this predicament. We can approximate the fractal using a random algorithm in the following way.

Begin with a single point (usually (0,0) is the easiest).  Then randomly choose a function in the system, and apply it to this point.  Then iterate:  keep randomly choosing a function from the system, then apply it to the last computed point.

What the theory says (again, read the Barnsley book for all the proofs!) is that these points keep getting closer and closer to the fractal image determined by the system.  Maybe the first few are a little off — but if we just get rid of the first 10 or 100, say, and plot the rest of the points, we can get a good approximation to the fractal image.

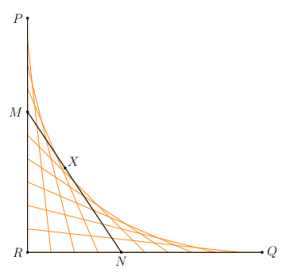
Consider the Sierpinski triangle again.  Below is what the first 20 points look like (after (0,0)), numbered in the order in which they’re produced.

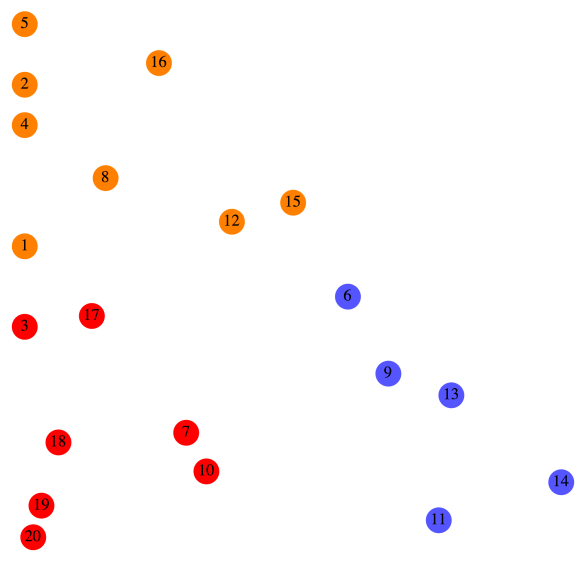
Let’s look at this in a bit more detail.  For reference, we’ll copy the function system which produces the Sierpinski triangle from the first post.

Now here’s how the color scheme works.  Any time is randomly chosen, the point is colored red.  For example, you can see that after Point 6 was drawn, was chosen, so Point 7 was simply halfway between Point 6 and the origin.

Any time is chosen, the point is colored blue.  For example, after Point 8 was drawn, was randomly chosen.  You can see that if you move Point 8 halfway to the origin and then over right one unit, you land up exactly at Point 9.

Finally, any time is chosen, the point is colored orange.  So for example, it should be clear that moving Point 7 halfway toward the origin and then up one unit results in Point 8.

Of course plotting more points results in a more accurate representation of the fractal.  Below is an image produced using 5000 points.

To get more accuracy, simply increase the number of points, but decrease the size of the points (so they don’t overlap).  The following image is the result of increasing the number of points to 50,000, but using points of half the radius.

There’s just one more consideration, and then we can move on to the Python code for the algorithm.  How do we randomly choose the next affine transformation?

Of course we use a random number generator to select a transformation.  In the case of the Sierpinski triangle, each of the three transformations had the same likelihood of being selected.

Now consider one of the fractals we looked at last week.

If the algorithm chose either transformation with equal probability, this is what our image would look like:

Of course there’s a huge difference!  What’s happening is that transformation actually corresponds to a much smaller portion of the fractal than — and so to get a more realistic idea of what the fractal is really like, we need to choose it less often.  Otherwise, we overemphasize those parts of the fractal corresponding to the effect of

Again, according to the theory, it’s best to choose probabilities roughly in proportion to the portions of the fractal corresponding to the affine transformations.  So rather than a 50/50 split, I chose 87.5% of the time, and just 12.5% of the time.  As you’ll see when you experiment, a few percentage points may really impact the appearance of a fractal image.

From a theoretical perspective, it actually doesn’t matter what the probabilities are — if you let the number of points you draw go to infinity, you’ll always get the same fractal image!  But of course we are limited to a finite number of points, and so the probabilities do in fact strongly influence the final appearance of the image.

So once you’ve chosen some transformations, that’s just the beginning.  You’ve got to decide on a color scheme, the number of points and their size, as well as the probabilities that each transformation is chosen.  All these choices impact the result.

Now it’s your turn!  Here is the Sage link to the python code which you can use to generate your own fractal images.  (Remember, you’ve got to copy it into one of your own Projects first.)  Freely experiment — I’ve also added examples of non-affine transformations, as well as affine transformations in three dimensions!

And please comment with interesting images you create.  I’m interested to see what you can come up with!

Most of us have probably created a mathematical envelope, although we likely didn’t call it that.  Below is an example which may easily be sketched on a piece of graph paper.  You can see the “move one up/down, move one left/right” method of determining the ends of the line segments.  I created this envelope of lines using Python — we’ll look at the code later so you can make some of your own.

I first began sketching envelopes when I was an undergraduate.  Of course they were aesthetically quite interesting — but as a mathematician, you cannot help but ask exactly what curve you’re approximating by drawing an envelope of lines.

Although it seems that you might be drawing tangents to a circular arc, this is not the case.  By continuing the pattern of moving one up/down and left/right, the envelope in the first quadrant develops into the following figure.

You can fairly easily see a parabola forming — and this parabola is in fact the curve whose tangents we drew on our graph paper.

How can we prove this?  We need a theorem about tangents to parabolas, which we state as it applies to the case at hand, as shown below.

Here is how the theorem goes.  Suppose P and Q are points on a parabola whose tangents intersect at R.  If X is a point on the parabola between P and Q, and if the tangent at X intersects PR at M and QR at N, then

[PM] / [MR] = [MX] / [XN] = [RN] / [NQ],

where we use “[AB]” to mean the length of the segment AB.  But in our case, [PR] = [QR], so this means that

[PM] = [RN]  and  [MR] = [NQ],

which validates our “one down, one right” method of creating endpoints of tangent segments.  This is because by moving down one and right one, we are preserving the relationship [PM] = [RN], and hence also [MR] = [NQ].

For the curious reader, this helpful theorem about tangents to parabolas is very nicely proved by Steven Taschuk in his Notes on tangents to parabolas on p. 5 (where the names of points in my diagram above correspond to the names of points in his proof of the theorem).

So they’re parabolas!  Not what you’d expect at first glance.

Of course back when I was beginning college, there was no easy way to create desktop graphics, and so I used the tried and true pen-and-paper method.  I took a photo of one of my favorites from that time period.

Drawing these figure takes patience and concentration.  I distinctly recall the first draft of this piece.  If you look at the left square, you’ll notice that the blue lines look like they’re underneath the red lines.  This isn’t hard to do — just draw the red lines first, and then when drawing the blue lines, just stop at the red and continue after.  But I lost focus for just a second, and drew a blue line right over the red lines — and then had to start over.  There was no erasing.

For those of you who want to try creating images by hand, a word about technique.  When using an ink pen, the ink tends to blot — and if you drag the pen along a ruler, you might get end up with a smear of ink.  So keep a napkin or paper towel handy, and wipe the tip of your pen on the paper towel after drawing each line.  It’ll save you a lot of grief.

Despite the relatively simple method of drawing envelopes of lines, there is ample room for creativity.  Here is a computer-generated version of a drawing dated December 24, 1986.  It’s another of my favorites, and I love the effect of bright color against black.

There’s no reason to stop at purely geometrical designs, either.  Here is an abstract half-face of a tiger, created with a simulated graph paper background.

And then there’s polar graph paper!  When you wanted a graph, well, you just drew it — there was no graphing calculator/computer to do it for you.  So you had graph paper handy.  Below is a design I created just for this post, based on some older sketches.

Here’s another image based on a sketch made on polar graph paper.

It’s been really interesting to experiment with the computer, since designs which might have taken hours to draw can be rendered in a few seconds (after you’ve done the programming, of course).

Envelopes are not restricted to being created by lines, however.  The figure below creates a cardioid from tangent circles.

A base circle (in red) is given, and a point on the circle is selected (the white point at the left).  Now for every other point on the circle (like the red point), create a circle by using that point and the white point as ends of a diameter of the circle (drawn in black).  These circles are internally tangent to a cardioid.

I don’t have room for the proof of this construction here, but there is a very nice book called Envelopes by Boltyanskii (just google it) which illustrates many additional examples of envelopes as well as techniques to determine what the resulting curve is.  Some of the techniques do involve calculus, so be forewarned!  This book was my real introduction to a study of mathematical envelopes.

Now it’s time for you to create your own envelopes!  You can click on the Sage link to follow along and alter the code as you see fit.

The routines aren’t really too complex.  Note the use of vectors in Python to make working with the mathematics fairly simple.  This is so we can compute the endpoints of the segments of the envelope easily.  The mathematics involved is illustrated in the following figure.

It looks more complicated than it is.  Since is between and we may write as a weighted average of and  We must do so in such a way that gives the point and is just above

Similarly, is a weighted average of and and must be such that is just to the right of and  Take a moment to study the figure and see that it all works out.  Note that the variables in the code mimic those in the figure exactly, so at least there is visual proof that the labels are correct!

So I’ll leave you to go ahead and experiment.  Feel free to comment with images you create using the Python code.  And stay tuned for next week, when I’ll talk about creating random envelopes.  There’s some really interesting stuff going on there….

Last week, we began exploring the piece Evaporation.  In particular, we looked at two aspects of the piece — randomness of both the colors and the sizes of the circles — and experimented with these features in Python.  Look at last week’s post for details!

Today, we’ll examine the third significant aspect of the piece — the color gradient.  The piece is a pure sky blue at the top, but becomes more random toward the bottom.  How do we accomplish this?

Essentially, we need to find a way to introduce “0” randomness to each color at the top, and more randomness as we move toward the bottom.  To understand the concept, though, we’ll be introducing 0 randomness at the bottom, and more as we move up.  You’ll see why in a moment.

Let’s first look at a linear gradient.  Imagine that we’re working with a square — we can always scale later.  Here’s what it looks like:

The “linear” part means we’re looking at randomness as a function of  So when we subtract randomness to each color.  But when we subtract a random number between and from each of the RGB values.  Finally, at the very top, we’re subtracting a random number between and from each RGB value.  Recall that if an RGB value would ever fall below as a result of subtraction, we’d simply treat the value as

Why do we subtract as we go up?  Recall that black has RGB values so subtracting the randomly generated number pushes the sky blue toward black.  If we added instead, this would push the sky blue toward white.  In fact, you can push the sky blue toward any color you want, but that’s a little too involved for today’s post.

The piece Evaporation was actually produced with a quadratic gradient.  Let’s look at a picture first:

That the gradient is quadratic means that the randomness introduced is proportional to for each value of  In other words, at a level of on our square, we subtract a random number between and

You can visually see this as follows.  Look at the gradient of color change from to for the quadratic gradient.  This is approximately the same color change you see in the linear gradient between and  Why does this happen?  Because when you square numbers less than they get smaller.  So smaller numbers will introduce less randomness in a quadratic gradient than they will in a linear gradient.

We can go the other way, we well.  If we use a quadratic gradient (exponent of ), the color changes more gradually at the bottom.  But if we use an exponent less than (such as in taking a root, like a square root or cube root), we get the opposite effect:  color changes more rapidly at the bottom.  This is because taking a root of a number less than  increases the number.  It’s easiest to see this with an example:

In this case, the exponent used is so that for a particular value, a random number between and is subtracted from each RGB value.  Note how quickly the color changes from the sky blue at the bottom toward very dark colors at the top.

Of course this is just one way to vary colors.  But I find it a very interesting application of power and root functions usually learned in precalculus — using computer graphics, we can directly translate an algebraic, functional relationship geometrically into a visual gradient of color.  Another example of why it is a good idea to enlarge your mathematical toolbox — you just never know when something will come in handy!  If I didn’t really understand how power and root functions worked, I wouldn’t have been able to create this visual effect so easily.

Now it’s your turn!  You can visit the Evaporation worksheet to try creating images on your own.  If you’ve been trying out the Python worksheets all along, the code should start to look familiar.  But a few comments are in order.

First, we just looked at a square.  It’s actually easier to think in terms of integer variables “width” and “height” (after all, there is no reason our image needs to be square).  In this case, we use “j” as the height parameter, since it is more usual to use variables like “i” and “j” for integers.  So “j/height” would correspond to  This would produce a color gradient of light to dark form bottom to top.

To make the gradient go from top to bottom, we use “(height-j)/height” instead (see the Python code).  This makes values near the top of the image correspond to and values near the bottom of the image correspond to  I’ll leave it to you to explore all the other details of the Python code.

Please feel free to comment with images you create using the Sage worksheet!

As mentioned in the previous post as well, each parameter you change — each number which appears anywhere in your code — affects the final image.  Some choices seem to give more appealing results than others.  This is where are meets technology.

As a final word — the work on creating fractals is still ongoing.  I’ve learned to make movies now using Processing:

You’ll notice how three copies of one fractal image morph into one of another.  You can find more examples on Twitter: @cre8math.  Once I feel I’ve had enough experience using Processing, I’ll post about how you can use it yourself.  The great thing about Processing is that you can use Python, so all your hard work learning Python will yield even further dividends!

This and the next post will walk you through how to create digital art similar to Evaporation.  I’ll also show you some Python code you can use yourself to experiment.

There are three significant features of Evaporation. First is the randomness of the colors. Second — if you look closely — the sizes of the circles are also different; these are randomly generated as well. The third feature is the gradient of the color — from a pure sky blue at the top, to a fairly randomly colored row of circles at the bottom. We’ll look at the first two features today.

Let’s look at color. In the figure above, the small teal square at the left has RGB values of 0, 0.5, and 0.7, respectively. The larger square at the left consists of 100 smaller squares. The color of each of these squares is generated by adding a random number between 0 and 0.1 to each of the RGB values 0, 0.5, and 0.7 — with a different random number added to each value. In the middle square, a random number between 0 and 0.2 is added, so this creates a wider range of color values. For the right square, the random numbers added are between 0 and 0.3.

But there is no reason that the ranges need to the same for each color. In the images below, the red values have a wider range of randomness then the green, which is “more random” than the blue.

You can see that different ranges of random numbers create different color “textures.” This is where I think computer meets art — as a programmer, when it comes to creating random numbers, you have to specify a range for the randomness of each variable. The choices you make determine how your image looks. How do you make “artistic” choices? There is no easy answer, of course.

Another way to use randomness is by varying the size of the graphic objects. In the left square below, texture is created by randomly changing the radii of the circles.

In the middle square, the circles are all the same size, but random shades of gray. The right square varies both the size of the circles and their color. The final result depends on “how much” randomness is used. You can try it for yourself by altering the Python code linked to below — change the randomness and see what happens!

I think of my laptop as an art laboratory. It is a place to experiment with different ideas — change this parameter, increase randomness, try out different color combinations. Can you imagine creating any of the images in this post by hand? The computer allows us to perform experiments unthinkable to Rembrandt and Van Gogh. We may lose the texture of brush strokes or the dimensionality of paint on canvas, but what we gain by having a programming language at our disposal makes up for this loss.  At least in my opinion….

Now let’s look at how we can use Python to create these images.  You can experiment with this color and texture worksheet.

There is not much more to say here since a lot is explained in the worksheet. But as you are creating, keep a few things in mind.

1. Use descriptive variable names. This helps a lot when you’re looking a lines of code. Using variables a, b, c, etc., doesn’t help much when you’re looking at a program you wrote a few months ago.

2. Comment liberally! Notes to yourself are easy to use in Python — just start a line (or part of a line) with the “\#” character. You’ll thank yourself later.

3.  Save versions often! I won’t bore you with stories of using Mathematica to do some intense computations for creating digital art — and then read the “Mathematica quit unexpectedly” message on my screen — before I saved my work. I’ve encountered this in Python, too — if you use the online version, you’re connecting to an external server, which hopefully will not encounter problems while you’re working….

Also, as you change parameters, you may want to keep track of results you like. If there are a lot of these, sometimes I write the parameters as comments — so I can reproduce them later. Very important: don’t forget to keep track of the random number seed you use! The feel and texture of an image can vary dramatically with the random number seed, so don’t ignore this vital parameter.

One final thought.  In creating this type of art, I keep in mind the tension between structure and randomness.  You can use the computer to create randomness — but if there’s too much randomness, the image doesn’t seem to hang together.  But if there’s too much structure, the image can lose its interesting texture, and appear flat and purely two-dimensional.  So the choice of parameters in creating randomness is fairly crucial in determining how the final image will look.  And as I’ve said before — this is where technology meets art.  It is fairly easy to create a computer-generated image — but not as easy to create computer-generated art.  The difference is not exactly easy to describe — and certainly opinions will differ.  It is the questions which arise in describing the difference which are intriguing and exciting.

Enough philosophizing. Time to begin the artistic process!  Feel free to comment by posting any images you create using the Python code.

Last week, we laid down some of the mathematical foundation needed to generate fractal images.  In this third and final post about creating fractals, we’ll discuss in some detail Python code you can adapt to making your own designs.  Follow along in this Sage notebook.

In order to produce fractal images iteratively, we need a function which returns the highest power of 2 within a positive integer (as discussed last week).  It is not difficult to write a recursive routine to do this, as is seen in the notebook.  This is really all we need to get started.  The rest involves creating the graphics.  I usually use PostScript for my images, like the one below discovered by Matthieu Pluntz.  There isn’t time to go into that level of detail here, though.

As far as the graphics are concerned, it would be nice to have an easily described color palette.  You might look here to find a wide range of predefined colors, which are available once we execute the “import mathplotlib” command (see Line 20).  These names are used in the “colors” variable.  Since each motif has four segments, I’ll color each one differently (though you may choose a different color scheme if you want to).

The loop is fairly straightforward.  On each iteration, first find the correct angle to turn using the highestpowerof2 function.  Then the segment to add on to the end of the path is

which represents converting from polar to rectangular coordinates.  This is standard fare in a typical high school precalculus course.  Note the color of the segment is determined by i % 4, since 0 is the index of the first element of any list in Python.

All there is left to do is output to the screen.  We’re done!  You can try it yourself.  But note that the way I defined the function, you have to make the second argument negative (compare the image in the notebook with last week’s post).  Be patient:  some of these images may take a few moments to generate.  It would definitely help the speed issue if you downloaded Sage on your own computer.

To create the image shown above, you need to use angles of 90 and -210 (I took the liberty of rotating mine 15 degrees to make it look more symmetrical).  To create the image below, angles of 90 and -250 are used.  However, 26,624 steps are needed to create the entire image!  It is not practical to create an image this complex in the online Sage environment.

How do you know what angles to use?  This is still an open question — there is no complete answer that I am aware of.  After my first post on October 4, Matthieu Pluntz commented that he found a way to create an infinite variety of fractal images which “close up.”  I asked him how he discovered these, and he responded that he used a recursive algorithm.  It would take an entire post just to discuss the mathematics of this in detail — so for now, we’ll limit our discussion to how to use this algorithm.  I’ve encoded it in the function “checkangles.”

To use this function, see the examples in the Sage notebook.  Be careful to enter angles as negative when appropriate!  Also, you need to enter a maximum depth to search, since perhaps the angles do not result in an image which “closes up,” such as with 11 and -169.  But here’s the difficult part mathematically — just because our algorithm doesn’t find where 11 and -169 closes up does not mean that the fractal doesn’t close.  And further, just because our algorithm produced a positive result does not mean the algorithm must close.  Sure, we’ve found something that produces many results with interesting images — which suggests we’re on the right track.  But corroboration by a computer program is not a proof.

At the end of the notebook, I wrote a simple loop illustrating how you can look for many possibilities to try at once.  The general rule of thumb is that the more levels required in the algorithm to produce a pair of angles (which is output to the screen), the more segments needed to draw it.  I just looked for an example which only required 5 levels, and it was fairly easy to produce.

So where do we go from here?  Personally, I’ve found this investigation fascinating — and all beginning from a question by a student who is interested in learning more about fractals.  I’ve tried to give you an idea of how mathematics is done in the “real world” — there is a lot of exploration involved.  Proofs will come later, but it is helpful to look at lots of examples first to figure out what to prove.  When I find out something significant, I’ll post about it.

And I will admit a recent encounter with the bane of a programmer’s existence — the dreaded sign error.  Yes, I had a minus sign where I should have had a plus sign.  This resulted in my looking at lots of images which did not close up (instead of closing up, as originally intended).  Some wonderful images resulted, though, like the one below with angles of 11 and -169.  Note that since the figure does not close up (as far as I know), I needed to stop the iteration when I found a sufficiently pleasing result.

If I hadn’t made this mistake, I might have never looked at this pair of angles, and never created this image.  So in my mind, this wasn’t really a “mistake,” but rather a temporary diversion along an equally interesting path.

I’ve been posting images regularly to my Twitter feed, @cre8math.  I haven’t even touched on the aesthetic qualities of these images — but suffice it to say that it has been a wonderful challenge to create interesting textures and color effects for a particular pair of angles.  Frankly, I am still amazed that such a simple algorithm — changing the two angle parameters used to create the Koch snowflake — produces such a wide range of intriguing mathematical and artistic objects.  You can be sure that I’m not finished exploring this amazing fractal world quite yet….