I decided, finally, to take the big plunge. I’ve been steadily working on my polyhedra textbook (I’ve discussed this in My Polyhedra Textbook, I and My Polyhedra Textbook, II), but ran into a bit of a snag. Since I wrote those posts, I self-published The Puzzle Cabaret, and given what I learned in the process, decided to self-publish my polyhedra book.
The snag? All my three-dimensional graphics are in color, and given that the book will approach 500 pages, would be prohibitively expensive to print in color. It would cost about $35 to print, but I want to sell it for less than that – the idea is for it not to be too expensive, so anyone with an interest in polyhedra can reasonably afford it. It would only cost about $6 to print in black and white.

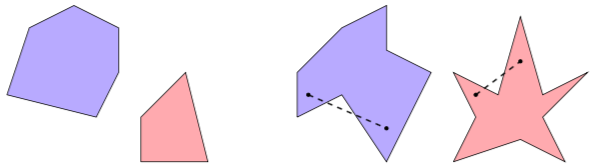
You might think, “Well, just convert to grayscale!” But what happens is that a brightly colored red tetrahedron, when converted to black and white, gives you a flat, dark gray tetrahedron — the one on the left — which is not very pleasing. And given that most polyhedra graphics on the web are similarly colored (and include some vertex/edge features which do not appeal to me), a simple conversion just won’t do. I’m looking for a tetrahedron with a little more contrast, like the one on the right.
So after a bit of work, that snag will eventually be fixed. I’ll have to redo the graphics one by one, but I have all the original code so I just need to change colors. Doable. But through conversations with Stacy (friend and design consultant), it seemed that for Part II of the book, it would be really nice to have images of all the uniform polyhedra. Really nice.
Well, I thought, that would be tons of work! Did I really think it would add that much to the book? Well, yeah, it probably would. There are programs/algorithms out there to produce polyhedra graphics, and it looked like it was time to take the plunge – dive into the inner workings of these programs and find a fairly simple way to produce the graphics. Sure, I could work them all out for myself – but data for some of the snub polyhedra require solving eighth-degree polynomials, and that’s just to get started!
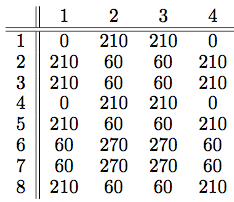
Turns out I hit the jackpot right away – and that never happens when you’re playing around with this stuff! I found this site, authored by David McCooey. For each uniform polyhedron – and its dual (when it exists) – he lists all the coordinates as well as which coordinates are vertices of which faces.
OK, that might seem like a lot of work, but I’ve worked with polyhedra graphics before. The idea is to use the symmetry of the polyhedron to help you out. So with the tetrahedron above, you just need to specify one face, and then “move it around.” In other words, use the symmetries (represented by 3-by-3 matrices) to create several different faces from one.
What this means is that you usually only need to specify vertices of a small number of faces, then copy them using symmetries to obtain the entire polyhedron. For example, the square and decagon below can be rotated and copied to yield the small rhombidodecahedron shown above.

So far, so good. But how do you represent the symmetries of a uniform polyhedron? Answering this question will be a major topic in this thread — I hope to walk you through a process of creating polyhedra graphics so you can try it on your own.
I’ll assume a basic familiarity with polyhedra – this thread would be impossibly long otherwise! In other words, I’ll assume that if you follow this thread, you’ve already played around with polyhedra a bit – built some, read some introductory books (like Magnus Wenninger’s Polyhedron Models, for example), and/or just stared at pictures of them, teasing out the various relationships among uniform polyhedra.
Also, I’ll need to assume some knowledge of Cartesian coordinates in three dimensions, as well as matrices and linear algebra. Anyone serious about 3D computer graphics needs this knowledge in their conceptual toolbox.
Finally, I’ll assume you’ve some programming platform you’re comfortable with which can produce three-dimensional graphics. I use Mathematica (which is not free), but I’ll discuss creating graphics from an algorithmic (rather than syntactic) point of view, so you can adapt to whatever program you’re using.

For today, I want to show you a few graphics which illustrate the basic geometry involved. If you’re very familiar with polyhedra, these ideas will not be new. But I think it’s important to include them for completeness.
The emphasis is on application, not theory. At the very least, a familiarity with abstract algebra (usually a senior-level course in an undergraduate math major) would be necessary to tackle the theory. That would be a completely different conversation, but not one for this thread.
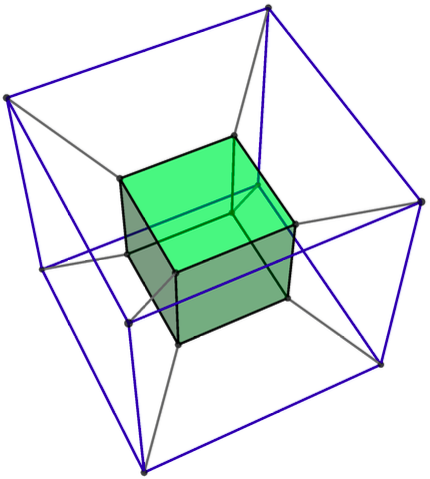
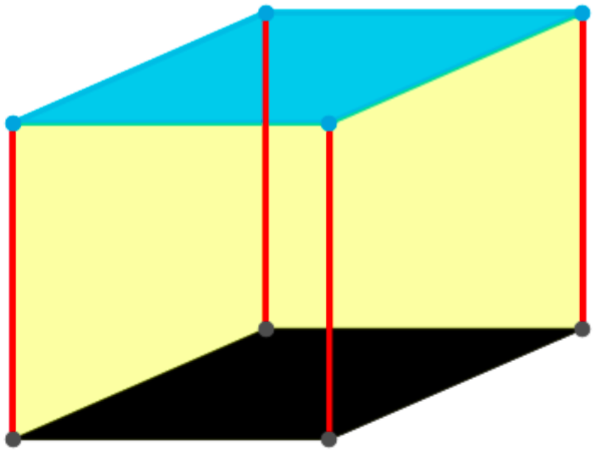
One important geometrical idea is that a tetrahedron can be inscribed in a cube, as shown below. This might not seem too amazing, but you can’t inscribe an equilateral triangle in a square in two dimensions.

Even more importantly, two tetrahedra can be inscribed in a cube, with no vertices left over. This is truly remarkable! Of course two equilateral triangles cannot be inscribed in a square (the two-dimensional analogue), and in higher dimensions (yes, four and higher!), this does not occur either. But in three dimensions, the simple equation 2 x 4 = 8 (four vertices on a tetrahedron and eight on a cube) works its subtle magic.

Moreover, the intersection of these two tetrahedra is an octahedron. Magic! Well, not really. It all derives from 2 x 4 = 8.
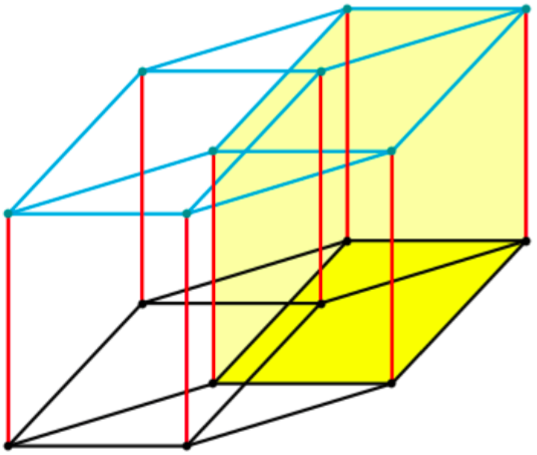
Another simple (but magic!) equation is 5 x 4 = 20. A tetrahedron has four vertices, while a dodecahedron has 20. It turns out that five tetrahedra may nicely be inscribed in a dodecahedron, as shown below. And the volume common to these five tetrahedra is an icosahedron.

If you look carefully, you can also see that a cube (shown in light gray below) can be inscribed in the same dodecahedron. This will be a great help in finding the matrices which represent the symmetries of the dodecahedron.

This sequence of a tetrahedron inscribed in a cube in inscribed in a dodecahedron is a special feature of three-dimensional geometry. And one reason why creating polyhedra graphics in three dimensions is actually a bit easier than you might think, as you’ll see in upcoming posts….